原始题目：剑指 Offer 51. 数组中的逆序对 (opens new window)

解题思路：

通过归并排序分治思想计算逆序对：

• 分：不断将数组进行二分，将整个数组的排序问题转化为子数组的排序问题；
• 治：当数组长度为 $1$ 时，开始向上合并，将 较短的排序数组 合并成 较长的排序数组，直到合并至原来数组时，完成排序；

合并阶段本质上是合并两个有序数组，可以在这个阶段进行逆序对的统计。下面假设合并到原来数组时，总体分为两个数组，左数组 $[0, 3]$ 和右数组 $[4, 7]$。

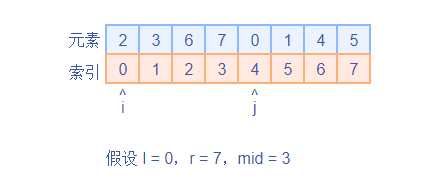
统计过程：

1. 使用指针$i$，$j$ ，初始值为 $i = 0$，$j = mid+1$。
2. 当 $i$ 指向的元素比 $j$ 指向的元素大时，则 ${nums[i], nums[j]}$组成一个逆序对。不但如此，因为两个子数组是有序的，所以实际上 $[i, mid]$ 之间的元素都可以与 $nums[j]$ 组成逆序对。因此，对于 $nums[j]$ 来说，有 $mid - i + 1$ 个逆序对。
3. 当 $i = 2$ 和 $j = 6$ 时，也是一样的计算方式。

将上述过程总结一下就是：

当合并左右子数组时，如果 左子数组当前元素 大于 右子数组当前元素时，意味着 [左子数组当前元素至末尾元素] 与 [右子数组当前元素] 构成 若干个 [逆序对]。

两个关键点就是：① 发生在合并两个有序子数组时；② 左子数组当前元素大于右子数组当前元素。

那么其实就是在归并排序的基础上，加上一行统计逆序对的代码即可。

代码：

private int ans = 0;

public int reversePairs(int[] nums) {
    mergeSort(nums, 0, nums.length - 1);
    return ans;
}

private void mergeSort(int[] nums, int l, int r) {
    if (l >= r) {
        return;
    }
    int mid = (l + r) / 2;
    mergeSort(nums, l, mid);
    mergeSort(nums, mid + 1, r);
    merge(nums, l, mid, r);
}

private void merge(int[] nums, int l, int mid, int r) {
    int[] tmp = new int[r - l + 1];
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r) {
        if (nums[i] <= nums[j]) {
            tmp[k++] = nums[i++];
        } else {
            // 计算逆序对，相比于归并排序，只多了这一句代码
            ans += mid - i + 1;
            tmp[k++] = nums[j++];
        }
    }
    while (i <= mid) {
        tmp[k++] = nums[i++];
    }
    while (j <= r) {
        tmp[k++] = nums[j++];
    }
    for (k = 0; k < tmp.length; k++) {
        nums[k + l] = tmp[k];
    }
}

复杂度分析

• 时间复杂度$O(NlogN)$：归并排序使用 $O(NlogN)$ 时间。
• 空间复杂度$O(N)$：整个过程创建辅助数组的长度为 $N$。